This example has been auto-generated from the examples/ folder at GitHub repository.

Gamma Mixture Model

# Activate local environment, see `Project.toml`
import Pkg; Pkg.activate(".."); Pkg.instantiate();

This notebook implements one of the experiments outlined in https://biaslab.github.io/publication/mp-based-inference-in-gmm/.

Load packages

using RxInfer, Random, StatsPlots

# create custom structure for model parameters for simplicity
struct GammaMixtureModelParameters
    nmixtures   # number of mixtures
    priors_as   # tuple of priors for variable a
    priors_bs   # tuple of priors for variable b
    prior_s     # prior of variable s
end

Model specification

@model function gamma_mixture_model(y, parameters)

    # fetch information from struct
    nmixtures = parameters.nmixtures
    priors_as = parameters.priors_as
    priors_bs = parameters.priors_bs
    prior_s   = parameters.prior_s

    # set prior on global selection variable
    s ~ Dirichlet(probvec(prior_s))

    # allocate variables for mixtures
    local as
    local bs

    # set priors on variables of mixtures
    for i in 1:nmixtures
        as[i] ~ Gamma(shape = shape(priors_as[i]), rate = rate(priors_as[i]))
        bs[i] ~ Gamma(shape = shape(priors_bs[i]), rate = rate(priors_bs[i]))
    end

    # allocate variables for local selection variable
    local z
    # specify local selection variable and data generating process
    for i in 1:length(y)
        z[i] ~ Categorical(s)
        y[i] ~ GammaMixture(switch = z[i], a = as, b = bs)
    end
    
end

constraints = @constraints begin 

    q(z, as, bs, s) = q(z)q(as)q(bs)q(s)

    q(as) = q(as[begin])..q(as[end])
    q(bs) = q(bs[begin])..q(bs[end])
    
    q(as)::PointMassFormConstraint(starting_point = (args...) -> [1.0])
end

Constraints: 
  q(z, as, bs, s) = q(z)q(as)q(bs)q(s)
  q(as) = q(as[(begin)..(end)])
  q(bs) = q(bs[(begin)..(end)])
  q(as) :: PointMassFormConstraint()

# specify seed and number of data points
rng = MersenneTwister(43)
n_samples = 2500

# specify parameters of mixture model that generates the data
# Note that mixture components have exactly the same means
mixtures  = [ Gamma(9.0, inv(27.0)), Gamma(90.0, inv(270.0)) ]
nmixtures = length(mixtures)
mixing    = rand(rng, nmixtures)
mixing    = mixing ./ sum(mixing)
mixture   = MixtureModel(mixtures, mixing)

# generate data set
dataset = rand(rng, mixture, n_samples);

# specify priors of probabilistic model
# NOTE: As the means of the mixtures "collide", we specify informative prior for selector variable
nmixtures = 2
gpriors = GammaMixtureModelParameters(
    nmixtures,                                                    # number of mixtures
    [ Gamma(1.0, 0.1), Gamma(1.0, 1.0) ],                         # priors on variables a
    [ GammaShapeRate(10.0, 2.0), GammaShapeRate(1.0, 3.0) ],      # priors on variables b
    Dirichlet(1e3*mixing)                                         # prior on variable s
)

gmodel         = gamma_mixture_model(parameters = gpriors)
gdata          = (y = dataset, )
init           = @initialization begin 
    q(s) = gpriors.prior_s
    q(z) = vague(Categorical, gpriors.nmixtures)
    q(bs) = GammaShapeRate(1.0, 1.0)
end
greturnvars    = (s = KeepLast(), z = KeepLast(), as = KeepEach(), bs = KeepEach())

goptions = (
     
    default_factorisation = MeanField() # Mixture models require Mean-Field assumption currently
)

gresult = infer(
    model          = gmodel, 
    data           = gdata,
    constraints    = constraints,
    options        = (limit_stack_depth = 100,),
    initialization = init,
    returnvars     = greturnvars,
    free_energy    = true,
    iterations     = 250, 
    showprogress   = true
);

# extract inferred parameters
_as, _bs = mean.(gresult.posteriors[:as][end]), mean.(gresult.posteriors[:bs][end])
_dists   = map(g -> Gamma(g[1], inv(g[2])), zip(_as, _bs))
_mixing = mean(gresult.posteriors[:s])

# create model from inferred parameters
_mixture   = MixtureModel(_dists, _mixing);

# report on outcome of inference
println("Generated means: $(mean(mixtures[1])) and $(mean(mixtures[2]))")
println("Inferred means: $(mean(_dists[1])) and $(mean(_dists[2]))")
println("========")
println("Generated mixing: $(mixing)")
println("Inferred mixing: $(_mixing)")

Generated means: 0.3333333333333333 and 0.33333333333333337
Inferred means: 0.3403381684590915 and 0.33433403819293
========
Generated mixing: [0.18923488676601088, 0.8107651132339891]
Inferred mixing: [0.11672347733753413, 0.8832765226624658]

# plot results
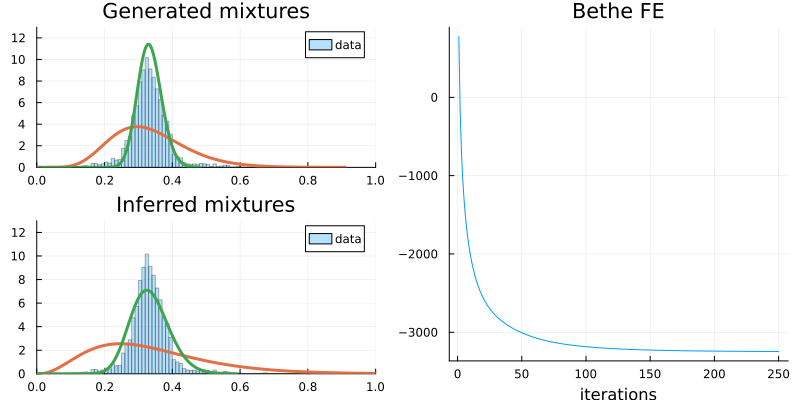
p1 = histogram(dataset, ylim = (0, 13), xlim = (0, 1), normalize=:pdf, label="data", opacity=0.3)
p1 = plot!(mixture, label=false, title="Generated mixtures", linewidth=3.0)

p2 = histogram(dataset, ylim = (0, 13), xlim = (0, 1), normalize=:pdf, label="data", opacity=0.3)
p2 = plot!(_mixture, label=false, title="Inferred mixtures", linewidth=3.0)

# evaluate the convergence of the algorithm by monitoring the BFE
p3 = plot(gresult.free_energy, label=false, xlabel="iterations", title="Bethe FE")

plot(plot(p1, p2, layout = @layout([ a; b ])), plot(p3), layout = @layout([ a b ]), size = (800, 400))