This example has been auto-generated from the examples/ folder at GitHub repository.
Simple Nonlinear Node
# Activate local environment, see `Project.toml`
import Pkg; Pkg.activate(".."); Pkg.instantiate();using RxInfer, Random, StableRNGsHere is an example of creating custom node with nonlinear function approximation with samplelist.
Custom node creation
struct NonlinearNode end # Dummy structure just to make Julia happy
struct NonlinearMeta{R, F}
rng :: R
fn :: F # Nonlinear function, we assume 1 float input - 1 float output
nsamples :: Int # Number of samples used in approximation
end@node NonlinearNode Deterministic [ out, in ]We need to define two Sum-product message computation rules for our new custom node
- Rule for outbound message on
outedge given inbound message oninedge - Rule for outbound message on
inedge given inbound message onoutedge - Both rules accept optional meta object
# Rule for outbound message on `out` edge given inbound message on `in` edge
@rule NonlinearNode(:out, Marginalisation) (m_in::NormalMeanVariance, meta::NonlinearMeta) = begin
samples = rand(meta.rng, m_in, meta.nsamples)
return SampleList(map(meta.fn, samples))
end# Rule for outbound message on `in` edge given inbound message on `out` edge
@rule NonlinearNode(:in, Marginalisation) (m_out::Gamma, meta::NonlinearMeta) = begin
return ContinuousUnivariateLogPdf((x) -> logpdf(m_out, meta.fn(x)))
endModel specification
After we have defined our custom node with custom rules we may proceed with a model specification:
\[\begin{aligned} p(\theta) &= \mathcal{N}(\theta|\mu_{\theta}, \sigma_{\theta}),\\ p(m) &= \mathcal{N}(\theta|\mu_{m}, \sigma_{m}),\\ p(w) &= f(\theta),\\ p(y_i|m, w) &= \mathcal{N}(y_i|m, w), \end{aligned}\]
Given this IID model, we aim to estimate the precision of a Gaussian distribution. We pass a random variable $\theta$ through a non-linear transformation $f$ to make it positive and suitable for a precision parameter of a Gaussian distribution. We, later on, will estimate the posterior of $\theta$.
@model function nonlinear_estimation(y, θ_μ, m_μ, θ_σ, m_σ)
# define a distribution for the two variables
θ ~ Normal(mean = θ_μ, variance = θ_σ)
m ~ Normal(mean = m_μ, variance = m_σ)
# define a nonlinear node
w ~ NonlinearNode(θ)
# We consider the outcome to be normally distributed
for i in eachindex(y)
y[i] ~ Normal(mean = m, precision = w)
end
end@constraints function nconstsraints(nsamples)
q(θ) :: SampleListFormConstraint(nsamples, LeftProposal())
q(w) :: SampleListFormConstraint(nsamples, RightProposal())
q(θ, w, m) = q(θ)q(m)q(w)
endnconstsraints (generic function with 1 method)@meta function nmeta(fn, nsamples)
NonlinearNode(θ, w) -> NonlinearMeta(StableRNG(123), fn, nsamples)
endnmeta (generic function with 1 method)@initialization function ninit()
q(m) = vague(NormalMeanPrecision)
q(w) = vague(Gamma)
endninit (generic function with 1 method)Here we generate some data
nonlinear_fn(x) = abs(exp(x) * sin(x))nonlinear_fn (generic function with 1 method)seed = 123
rng = StableRNG(seed)
niters = 15 # Number of VMP iterations
nsamples = 5_000 # Number of samples in approximation
n = 500 # Number of IID samples
μ = -10.0
θ = -1.0
w = nonlinear_fn(θ)
data = rand(rng, NormalMeanPrecision(μ, w), n);now that synthetic data/constriants/model is defined, lets infer:
result = infer(
model = nonlinear_estimation(θ_μ = 0.0, m_μ = 0.0, θ_σ=100.0, m_σ=1.0),
meta = nmeta(nonlinear_fn, nsamples),
constraints = nconstsraints(nsamples),
data = (y = data, ),
initialization = ninit(),
returnvars = (θ = KeepLast(), ),
iterations = niters,
showprogress = true
)Inference results:
Posteriors | available for (θ)we can check the posterior now
θposterior = result.posteriors[:θ]SampleList(Univariate, 5000)Let's us visualise the results
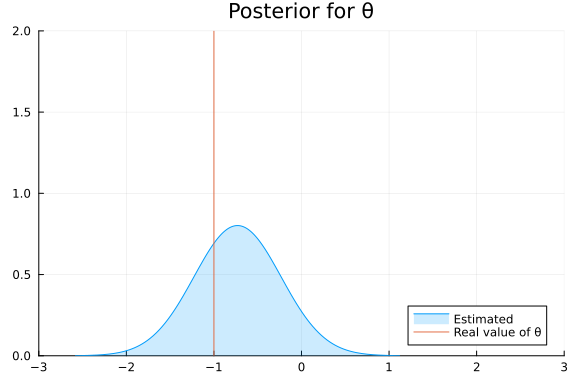
using Plots, StatsPlots
estimated = Normal(mean_std(θposterior)...)
plot(estimated, title="Posterior for θ", label = "Estimated", legend = :bottomright, fill = true, fillopacity = 0.2, xlim = (-3, 3), ylim = (0, 2))
vline!([ θ ], label = "Real value of θ")